Waves
Related chapter: Wave Phenomena
Syllabus
- 4.1 Oscillations
- Recognise simple harmonic motion (SHM).
- Describe the interchange of kinetic and potential energy involved within a cycle of SHM.
- Define SHM in words and in graph form.
- Interpret a–s graphs of SHM.
- Understand the terms time period, frequency and amplitude as applied to SHM.
- Use the equation T=f1, giving the frequency in Hertz.
- Sketch s–t, v–t and a–t graphs of SHM.
- Describe the phase difference between two oscillators with identical time periods.
- 4.2 Travelling waves
- Wavelength, frequency, period, and wave speed
- Solving problems involving wave speed, frequency, and wavelength.
- Guidance
- Students will be expected to derive c=fλ .
- Transverse and longitudinal waves
- Explaining the motion of particles of a medium when a wave passes through it for both transverse
and longitudinal cases.
- Sketching and interpreting displacement–distance graphs and displacement–time graphs for
transverse and longitudinal waves.
- 4.3 Wave characteristics
- Amplitude and intensity
- Solving problems involving amplitude and intensity.
- Superposition
- Sketching and interpreting the superposition of pulses and waves.
- Students will be expected to calculate the resultant of two waves or pulses both graphically and algebraically.
- Guidance
- Students will be expected to calculate the resultant of two waves or pulses both graphically and algebraically.
- Polarization
- Describing methods of polarization.
- 4.4 Wave Behaviour
- Reflection and refraction (light)
- Sketching and interpreting incident, reflected, and transmitted waves at boundaries between media.
- Solving problems involving reflection at a plane interface.
- Snell’s law, critical angle, and total internal reflection (light)
- Solving problems involving Snell’s law, critical angle, and total internal reflection.
- Determining refractive index experimentally.
- Guidance
- Quantitative descriptions of refractive index are limited to light rays passing between two or more transparent media. If more than two media, only parallel interfaces will be considered.
- 4.5 Standing Waves
- The nature of standing waves
- Describing the nature and formation of standing waves in terms of superposition. - Distinguishing between standing and travelling waves.
- Guidance
- Students will be expected to consider the formation of standing waves from the superposition of no more than two waves.
- Boundary conditions
- Sketching and interpreting standing wave patterns in strings.
- Guidance
- Boundary conditions for strings are: two fixed boundaries; fixed and free boundary; two free boundaries.
- Nodes and antinodes
- Solving problems involving the frequency of a harmonic, length of the standing wave, and the speed of the wave.
- Guidance
- The lowest frequency mode of a standing wave is known as the first harmonic - The terms fundamental and overtone will not be used.
Definitions
- A wave is a disturbance that travels in a medium, transferring energy and momentum from one place to another. The direction of propagation of the wave is the direction of energy transfer.
- A transverse wave is one in which the displacement is perpendicular to the direction of energy transfer.
- An oscillation is a cyclical (repeating) motion of an object. If the motion repeats in a fixed time interval it is called isochronous, and the time interval of repetition is called the period. An oscillation will have limits on its displacement from a central point.
- Simple harmonic motion is defined as motion arising from acceleration of an object that is proportional to its displacement from a fixed equilibrium point (rest position) and directed toward that point.F,a∝−x
- A restoring force (F) is any force that is proportional to the opposite of a displacement, which is responsible for bringing an object in SHM back to its equilibrium.
- The amplitude of a particle in SHM is the maximum displacement from equilibrium.
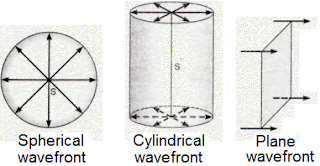
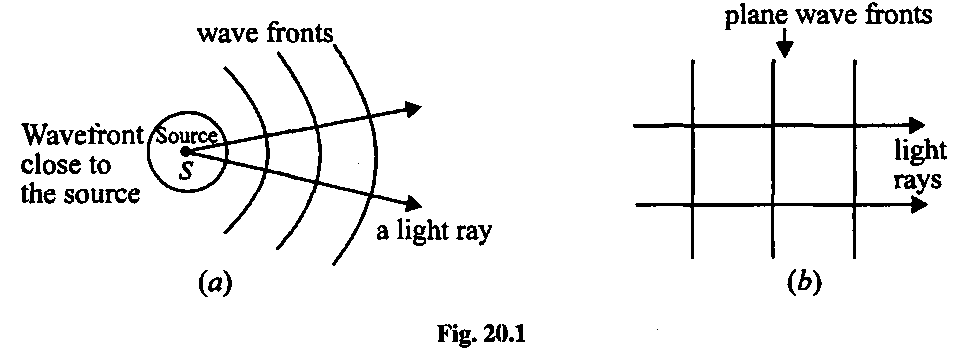
- A wavefront is a surface through crests and normal to the direction of energy transfer of the wave.
- Rays are lines at right angles to the wavefronts, and show the direction of wave propagation.
FfvEIIInmsin(θ1)sin(θ2)sin(θ1)λn=n2L;nλn=n4L;n=−kx=T1=fλ=EP+EK=aP=4πx2P=I0cos(θ)2=cmc=c1c2=n2sin(θ2)=1,2,3,4…(both ends free/fixed)=1,3,5,7…(one end free)
| Symbol |
What it represents |
Unit |
| F |
restoring force |
N |
| k |
spring constant |
Nm−1 |
| x |
displacement |
m |
| E |
total internal energy |
J |
| EK |
internal kinetic energy |
J |
| EP |
internal potential energy |
J |
| P |
power |
W |
| a |
area |
m2 |
| I |
intensity/transmitted intensity |
Wm−2 |
| x |
radius of the sphere in which a light source is emitting light |
m |
| I0 |
incident intensity on a polariser |
Wm−2 |
Theory
Simple Harmonic Motion
- Phase difference must be an integral multiple of π,π/2
- Wave properties
- Time period (T)
- Frequency
- Phase
- Phase difference
- In SHM without damping, the sum of EK and EP is constant. In other words, energy is conserved.
- Phase difference is the difference in synchronisation of two waves, expressed in radians.

- SHM can also be thought of as a one-dimensional projection of uniform circular motion:

Graphs of acceleration, velocity, and displacement

Relationship between EK and EP

Waves
- Each wave is simply a disturbance in a medium which transfers energy from one place to another. This is done by oscillating particles in the medium.
- Waves have the following characteristics:
- Wavelength: the length of a complete oscillation.
- Frequency: the number of times a complete oscillation is done in unit time.
- Time period: the time taken for one oscillation.
- Speed: how much distance each particle in the medium covers in unit time.
- Note: the speed of the wave depends only on the properties of the medium and not on how it is produced.
- Deriving v=fλ
- v=timedistance=λ⋅T1=fλ
Transverse waves
- In transverse waves, the direction of propagation is perpendicular to the movement of the particles in the medium.
- Examples are water waves, light (electromagnetic waves) , and waves on a guitar string.

- Each wave has a crest (position of maximum displacement) and a trough (position of minimum displacement).
- The amplitude of a transverse wave can be calculated by A=2position of crest−position of trough

Electromagnetic waves
- These are transverse waves composed of perpendicularly oscillating magnetic and electric fields.
- These waves move at the speed of light (299,792,458ms−1) in a vacuum.

- Electromagnetic waves are part of the electromagnetic spectrum, which contains the following categories of waves:

Longitudinal waves
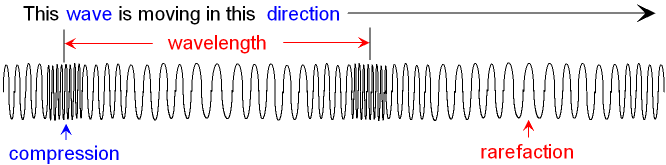
- In longitudinal waves, the direction of propagation is parallel to the direction of energy transfer.
- Examples are longitudinal waves along a spring, and sound.
- Sound waves:

- Longitudinal waves in a spring:

- Just like transverse waves have crests and troughs, longitudinal waves have compressions and rarefactions.
- Compressions are regions of the wave where particles are closest to each other.
- Rarefactions are regions of the wave where particles are furthest from each other.
Wavefronts and rays
- A wavefront is a surface through crests and normal to the direction of energy transfer of the wave.

- Rays are lines at right angles to the wavefronts, and show the direction of wave propagation.
Amplitude and intensity
- Each wave carries energy, and the rate at which the energy carried is the power (P) of the wave.
- Intensity is the power of the light source incident on area a, expressed in Wm−2. I=aP
- If a light source is emitting light in a spherical manner, then the light at a distance x away from the light source has intensity: I=4πx2P
- The intensity at a particular point is proportional to the power P of the light source. Referring to Wave Phenomena, we know that P∝Etotal∝A2, so I∝P∝Etotal∝A2I∝A2
Superposition
- The principle of superposition states that when two or more waves of the same type arrive at a given point in space at the same time, the displacement of the medium at that point is the algebraic sum of the individual displacements.
- Superposition can happen constructively or destructively.

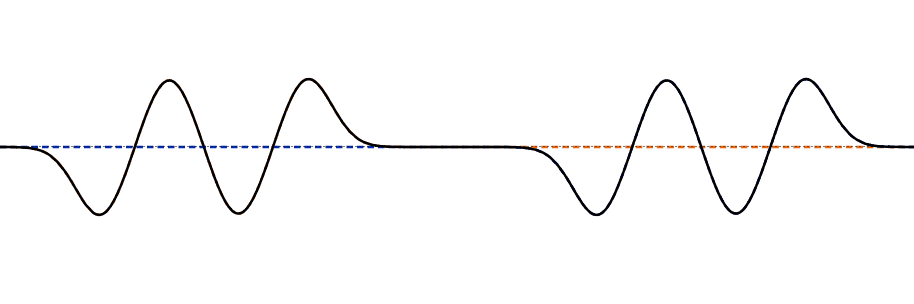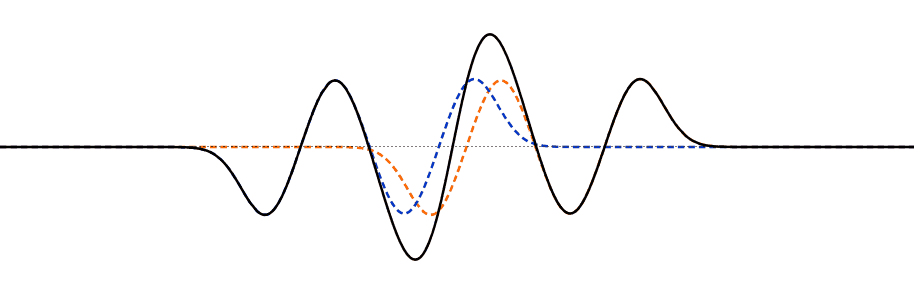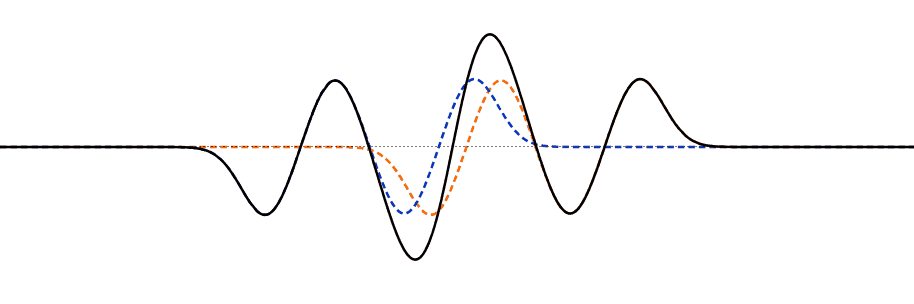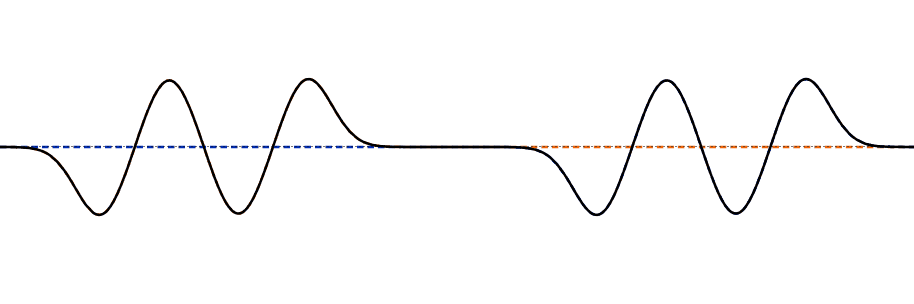
Reflection of pulses
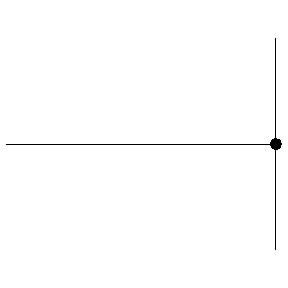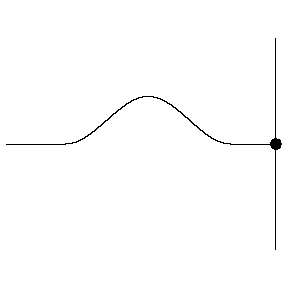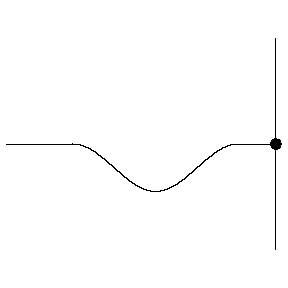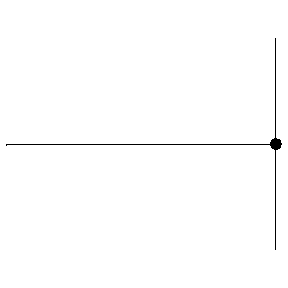
Reflection from a fixed end
- The pulse will be reflected by the fixed and become inverted.
- This is because the fixed end exerts an equal and opposite force on the string/rope, so an upward pulse now moves downward, and vice versa.
- This corresponds to a phase change of 180∘ or π radians when reflected.
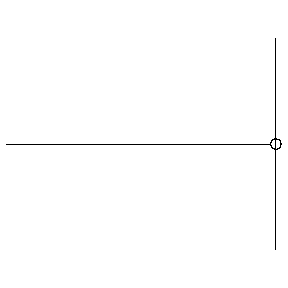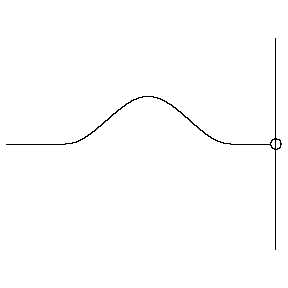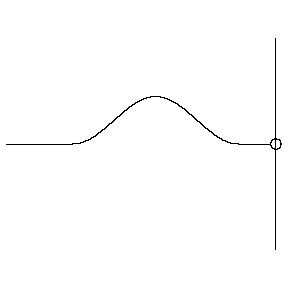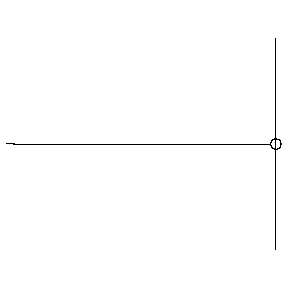
Reflection from a free end
- As the pulse arrives at the free end, the free end is pulled upwards. Once it falls back down, the pulse is sent back not inverted, so there is no phase change.
Polarisation
- An electromagnetic wave is said to be plane polarised if the electric field oscillates on the same plane.
- Individual emitters of light emit polarised light waves, but light from a large collection of individual emitters is unpolarised.
- A polariser is a sheet of material with a molecular structure that allows only a specific orientation of the electric field to pass through.

- The ray of light consisted of a large number of differently polarised waves before entering the polariser (the grey rectangle in the middle). After coming through the polariser, light was polarised, as the electric field oscillated on the same plane.
Malus’s Law
- When an electromagnetic field with electric field E0 passes through a polariser and makes an angle θ with the transmission axis. the transmitted electric field E will be E0cos(θ).
- This can be visualised as follows:

- Only the vertical component of E0 is transmitted, calculated by E0cosθ.
- Since I∝E2, we can assume I0=kE02 for some constant k. The new intensity would be I=kE2=k(E0cos(θ))2=kE02cos(θ)2=I0cos(θ)2.
- Therefore:
I=I0cos(θ)2 where I represents transmitted intensity and I0 represents incident intensity.
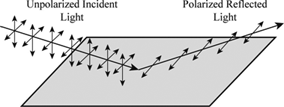
Polarisation by reflection
- When unpolarised light reflects off a non-metallic surface, the reflected ray is partially polarised.
- The reflected light has various components of electric field of unequal magnitude.
- The component with the greatest magnitude is found in the plane parallel to the surface.
Reflection
- When a ray reflects off a surface, the angle of incidence with the normal to the surface is equal to the angle of reflection.

Refraction
- Refraction is the travel of light from one medium into another.
- The refractive index of a particular medium with respect to another medium is the ratio of the speeds in the media.
- In refraction, the following laws are obeyed:
- nm=cmc
- sin(θ1)sin(θ2)=c1c2
- n1sin(θ1)=n2sin(θ2)
- Where:
- c is the speed of light in vacuum
- nm is the refractive index of medium m
- θ1 is the angle at the normal to the surface for the ray passing through medium 1
- θ2 is the angle at the normal to the surface for the ray passing through medium 2
- The medium in which light is relatively faster is called the optically rarer medium.
- The medium in which light is relatively slower is called the optically denser medium.
- Whenever refraction occurs, a small component of the incident ray is reflected.
Dispersion
- Rays with the same angle of incidence but differerent wavelengths are refracted at different angles. This is called dispersion.
- This means that n for water with respect to a vacuum for red light is different than n for water with respect to a vacuum for blue light.
- Light with shorter wavelength refract more (bend more), and light with longer wavelength refract less. This can be seen in the dispersion of white light in a prism.
Total Internal Reflection
- When light moves from a denser to a rarer medium, it diverges from the normal at a greater angle than the angle of incidence.
- The angle of incidence at which the angle of refraction is 90∘ is called the critical angle, θc.
- At any angle of incidence greater than θc, there is no refracted ray. The ray is completely reflected back into the medium. This is called total internal reflection.
- sinθc=n1
Diffraction
- Diffraction takes place when a wave with wavelength comparable to or larger than the size of an aperture or an obstacle moves through or past it and spreads out.
- The larger the wavelength is relative to the slit width , the greater the effect.
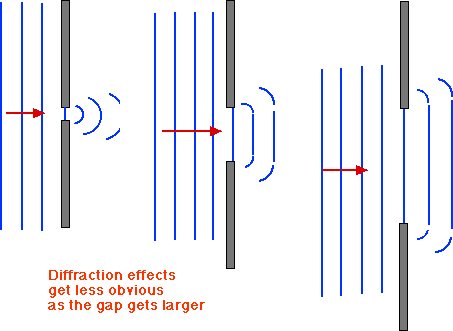
- If the aperture size equals the wavelength,the diffracted wavefronts are perfectly circular.

Interference
See Wave Phenomena for an explanation of single-slit and double-slit interference.
Standing Waves
- When two waves of the same speed, wavelength and amplitude meet, a standing wave is formed.
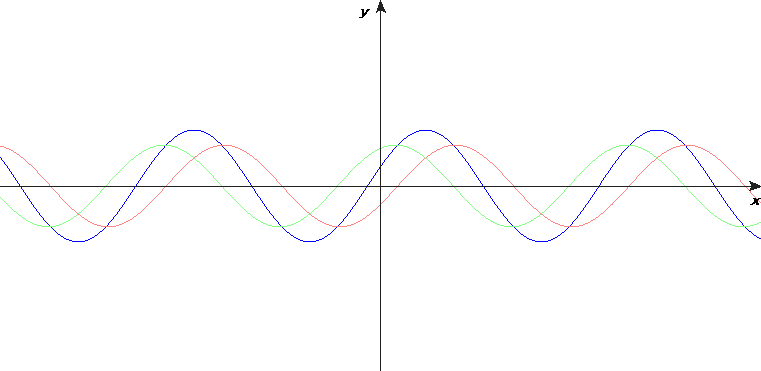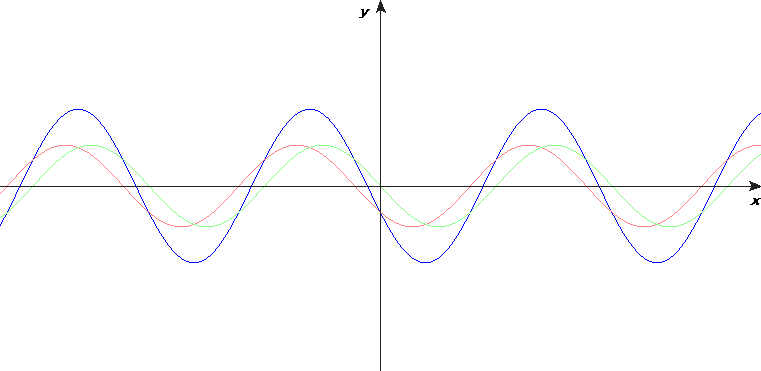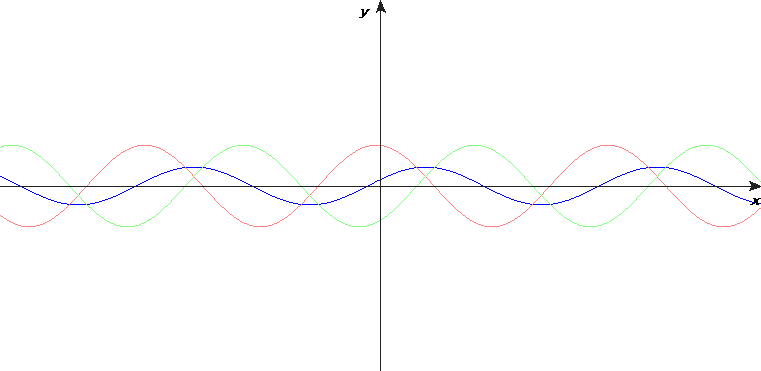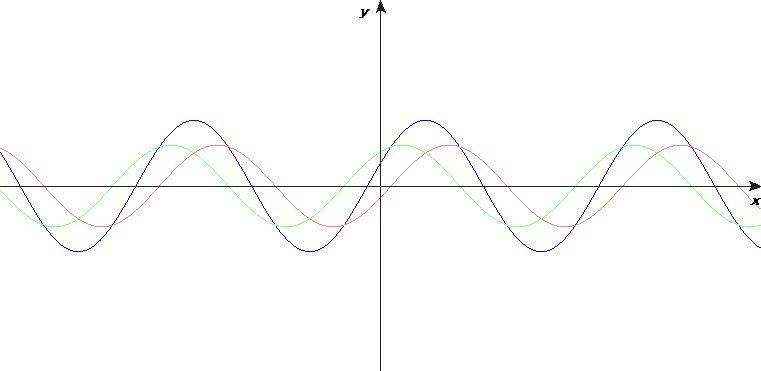
- Features of standing waves not seen in travelling waves:
- The crests and troughs stay at the same place.
- The points at which displacement is zero, nodes, do not move.
- Half-way points between nodes are where displacement is maximum. These are called antinodes.
- Points between consecutive nodes are in phase.
- Points in between the next pair of consecutive nodes have a velocity in the opposite direction of the points between a given pair.
- The amplitude of oscillation is different at different points on the string.
- A standing wave does not transfer energy.
- The ends of a standing wave are either nodes or antinodes. They determine the possible shape of the wave.
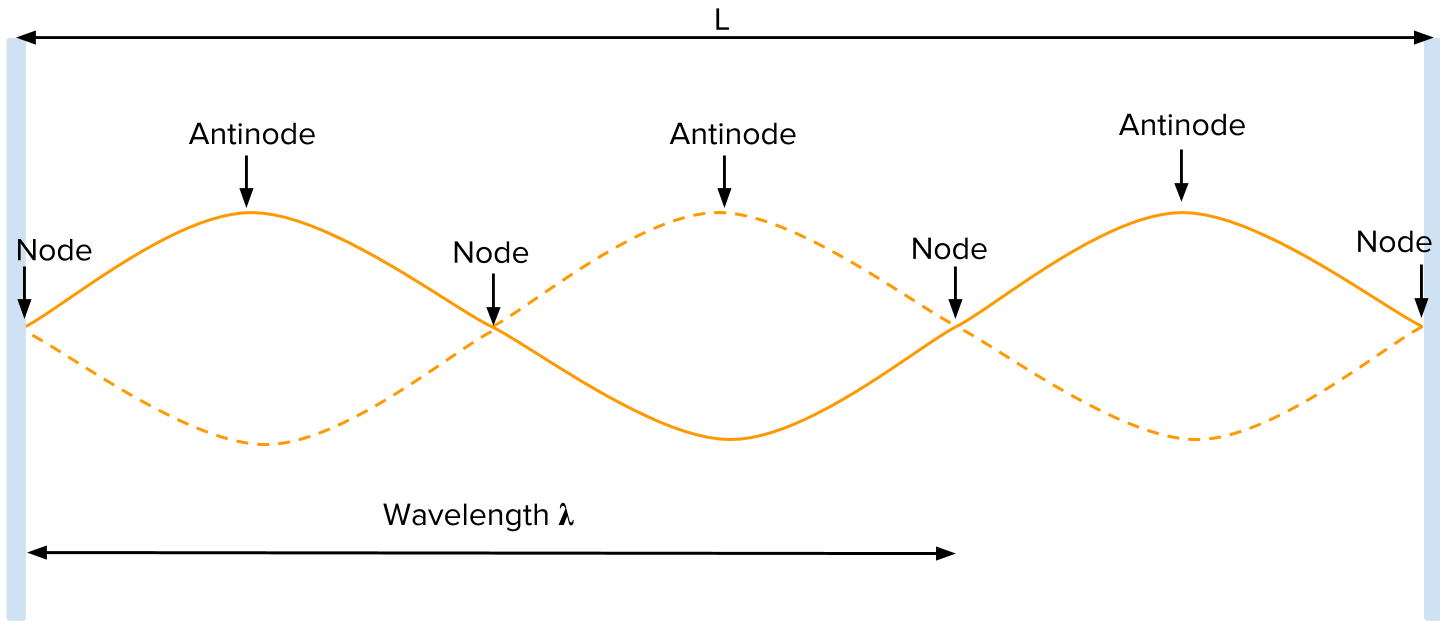
Standing Waves on Strings
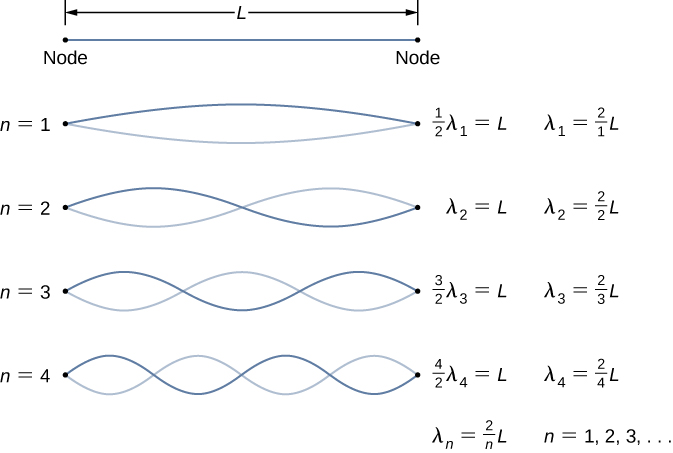
| Harmonic |
Number of nodes |
Number of Antinodes |
Wavelength |
| 1 |
2 |
1 |
2L |
| 2 |
3 |
2 |
22L |
| 3 |
4 |
3 |
32L |
| 4 |
5 |
4 |
42L |
| n |
n+1 |
n |
n2L |
- The first harmonic has the lowest frequency, as it has the highest wavelength.
- All harmonics have frequencies that are integral multiples of the first harmonic.
Standing Waves in Pipes
Pipe with both ends open
- The end conditions for this pipe are antinode-antinode.
- λn=n2L,n∈{1,2,3,4,5,6,…}
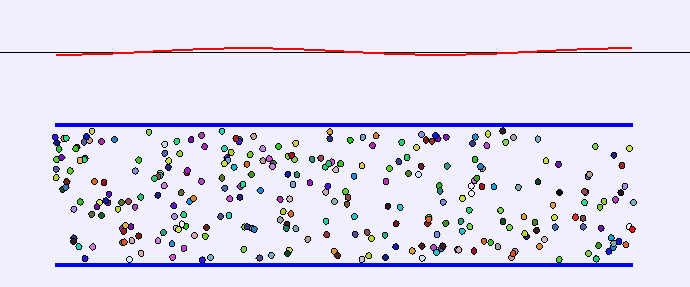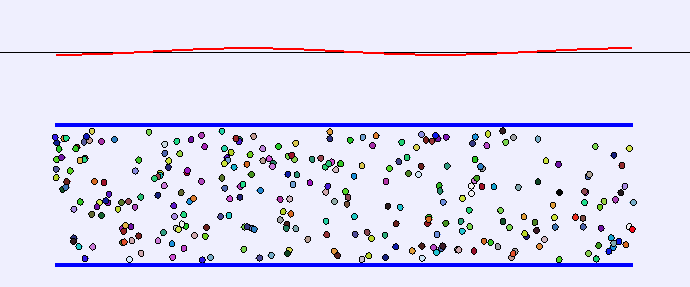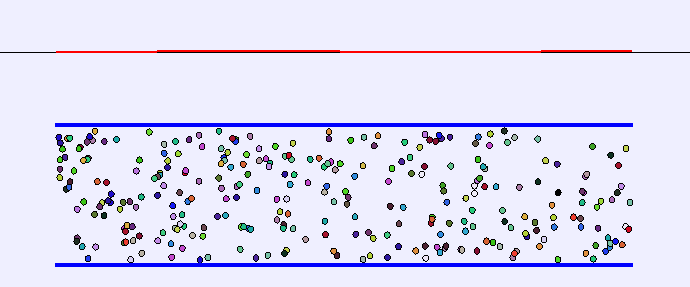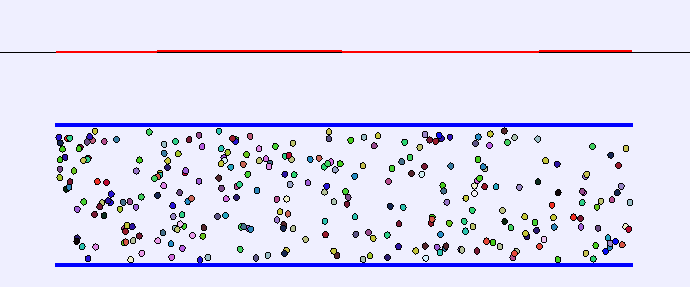
Pipe with one end open
- The end conditions for this are antinode-node.
- There are only “odd” harmonics present here.
- λn=n4L,n∈{1,3,5,7,9,11…}

Pipe with both ends closed
- The end conditions for this are node-node.
- λn=n2L,n∈{1,2,3,4,5,6,…}
References